L1, L2 Norm / Regularization

Source: https://commons.wikimedia.org/wiki/File:Regularization.jpg

*본 게시글은 유튜브 ‘혁펜하임 AI & 딥러닝 강의’ 선대 2-4강. 벡터의 norm 쉬운 설명과 ‘신박Ai’ [Deep Learning 101] L1, L2 Regularization 자료를 참고한 점임을 알립니다.

Norm

• Norm은 벡터의 크기(또는 길이)나 두 벡터 간의 거리를 나타냅니다.

\[\|\mathbf{x}\|_p = \left( \sum_{i=1}^{n} |x_i|^p \right)^{\frac{1}{p}}\]

• \(x\)는 n차원의 벡터입니다.

• \(p\)는 양수이며, 노름의 종류를 결정합니다.

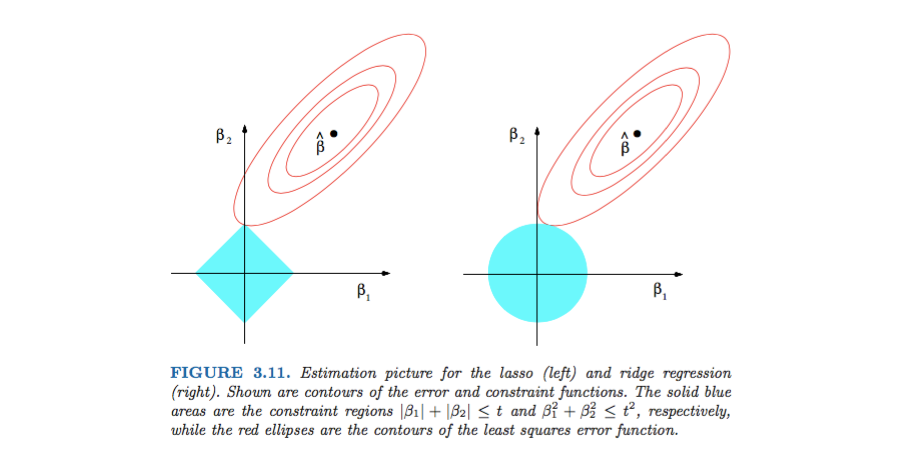
• 2차원 공간에서 단위 원(unit circle)으로 생각해보면 L1 / L2 Norm은 기하학적으로 다른 특성을 가지고 있습니다.

• L1 Norm의 단위 원은 마름모 형태입니다.

\[|x₁| + |x₂| = 1\]

• L2 Norm의 단위 원은 실제 원 형태입니다.

\[x₁² + x₂² = 1\]

• 이런 기하학적 차이가 정규화 과정에서도 중요한 차이를 만들어냅니다.

1. L1 Norm

\[\|\mathbf{x}\|_1 = \sum_{i=1}^{n} |x_i|\]

• \(L1\ Norm\)은 \(p=1\)일 때의 경우입니다.
• 맨해튼 노름(Manhattan Norm) 또는 택시캡 노름(Taxicab Norm)이라고도 불립니다.
• 이는 벡터의 각 성분의 절댓값을 더한 값으로 정의됩니다.
• 주로 특성이 희소한 벡터(즉, 대부분의 성분이 0인 벡터)를 다룰 때 유용합니다.
• 머신 러닝에서 특성 선택(Feature Selection) 또는 정규화(Regularization)에 자주 사용됩니다.

2. L2 Norm

\[\|\mathbf{x}\|_2 = \left( \sum_{i=1}^{n} |x_i|^2 \right)^{\frac{1}{2}} = \sqrt{\sum_{i=1}^{n} x_i^2}\]

• \(L2\ Norm\)은 \(p=2\)일 때의 경우입니다.
• 유클리드 노름(Euclidean Norm)이라고 불리며, 이는 벡터의 유클리드 거리, 즉 벡터의 각 성분을 제곱한 값들의 합의 제곱근으로 정의됩니다.
• 주로 거리 측정에서 많이 사용됩니다. 예를 들어, 두 벡터 사이의 유클리드 거리는 그 벡터들의 차이 벡터의 \(L2\ Norm\)으로 계산할 수 있습니다.
• 머신 러닝에서 정규화(Regularization)에 사용되며, Ridge 회귀에서는 \(L2\ Norm\)을 사용하여 계수를 규제하여 과적합을 방지합니다.

3. Infinite Norm

\[\|\mathbf{x}\|_\infty = \max_{i} |x_i|\]

• \(L∞\ Norm\)은 \(p=∞\)일 때의 경우입니다.

Regularization

• Regularization은 딥러닝 및 머신러닝에서 모델의 과적합을 방지하고 일반화 성능을 향상시키기 위해 사용되는 기법입니다.
• 정규화(Regularization)는 모델의 복잡성을 제한하여 훈련 데이터에 과도하게 적합되는 것을 방지합니다. 일반적으로 \(L1\ Regularization\)와 \(L2\ Regularization\) 정규화가 많이 사용됩니다.
• 정규화(Regularization) 기법은 모델의 손실 함수에 추가적인 항을 추가하여 모델의 가중치에 제약을 두는 방식으로 작동합니다.

1. L1 Regularization

• 선형 회귀 모델 정의

\[\hat{y} = wx + b\]

• 손실 함수 정의 \(\text{MSE} = \frac{1}{N} \sum_{j=1}^{N} (\hat{y}_j - y_j)^2\)

\[(N: 데이터 포인트의 총 개수,\ \hat{y}_j: 모델의 예측 값, \ y_j: 실제 값)\]

• L1 Regularization 수식 전개 \(L_1 = \text{MSE} + \lambda |w|\)

\[L_1 = (\hat{y} - y)^2 + \lambda |w|\] \[L_1 = (wx + b - y)^2 + \lambda |w|\] \[\frac{\partial L_1}{\partial w} = (1)\frac{\partial}{\partial w}[(wx + b - y)^2] + (2)\ \lambda \frac{\partial}{\partial w}|w|\] \[(1)\ \frac{\partial}{\partial w}[(wx + b - y)^2] = 2(wx + b - y) \cdot x\] \[(2) \ \frac{\partial}{\partial w}|w| = \begin{cases} + \lambda & \text{if } w > 0 \\ - \lambda & \text{if } w < 0 \\ \end{cases}\] \[\frac{\partial L_1}{\partial w} = 2(wx + b - y) \cdot x + \begin{cases} + \lambda & \text{if } w > 0 \\ - \lambda & \text{if } w < 0 \\ \end{cases}\]

• 가중치 업데이트

\[w^* = w - \alpha \frac{\partial L_1}{\partial w}\] \[(\alpha: Learning\ rate)\] \[w^* = w - \alpha \left(2(wx + b - y) \cdot x + \begin{cases} + \lambda & \text{if } w > 0 \\ - \lambda & \text{if } w < 0 \\ \end{cases}\right)\]

• L1 Regularization는 가중치가 양수일 때는 \(λ\)를 더하고, 음수일 때는 \(λ\)를 빼는 방식으로 작용합니다. 그 결과, 일부 가중치 \(w\)는 0으로 수렴하게 됩니다. 이렇게 가중치가 0으로 수렴함으로써 모델의 희소성이 증가하게 됩니다.

• 희소성 유도: 가중치가 0이 되는 특성이 많아지면서, 모델은 불필요한 특성을 자동으로 제거하게 됩니다.

• 해석 가능성 향상: 가중치가 0이 아닌 특성만 남게 되어, 어떤 특성이 모델에 중요한지를 쉽게 파악할 수 있습니다.

• 특성 선택: L1 정규화는 자연스럽게 특성 선택의 역할을 수행하여, 모델의 성능을 향상시키고 과적합을 방지합니다.

2. L2 Regularization

• 선형 회귀 모델 정의

\[\hat{y} = wx + b\]

• 손실 함수 정의

\[\text{MSE} = \frac{1}{N} \sum_{j=1}^{N} (\hat{y}_j - y_j)^2\] \[(N: 데이터 포인트의 총 개수,\ \hat{y}_j: 모델의 예측 값, \ y_j: 실제 값)\]

• L2 Regularization 수식 전개

\[L_2 = \text{MSE} + \lambda w^2\] \[L_2 = (\hat{y} - y)^2 + \lambda w^2\] \[L_2 = (wx + b - y)^2 + \lambda w^2\] \[\frac{\partial L_2}{\partial w} = (1)\frac{\partial}{\partial w}[(wx + b - y)^2] + (2)\ \lambda \frac{\partial}{\partial w}w^2\] \[(1)\ \frac{\partial}{\partial w}[(wx + b - y)^2] = 2(wx + b - y) \cdot x\] \[(2) \ \frac{\partial}{\partial w}w^2 = 2\lambda w\] \[\frac{\partial L_2}{\partial w} = 2(wx + b - y) \cdot x + 2\lambda w\]

• 가중치 업데이트

\[w^* = w - \alpha \frac{\partial L_2}{\partial w}\] \[(\alpha: Learning\ rate)\] \[w^* = w - \alpha \left(2(wx + b - y) \cdot x + 2\lambda w\right)\]

• L2 Regularization는 가중치가 클수록 그 제곱값에 비례해 가중치에 페널티를 부과합니다. 그 결과, 모든 가중치 ( w )가 0에 가깝게 작아지지만, 완전히 0이 되지는 않습니다.

• 가중치 감소: L2 Regularization는 모든 가중치를 작게 만들어 모델이 복잡해지지 않도록 합니다.

• 해석 가능성 향상: 가중치가 작아짐으로써, 과도하게 영향을 미치는 특성을 방지하고, 모델의 해석 가능성을 높입니다.

• 과적합 방지: L2 정규화는 모델의 복잡성을 줄이고, 데이터에 대한 과적합을 방지하여 더 나은 일반화 성능을 갖도록 합니다.

참고 자료

• https://commons.wikimedia.org/wiki/File:Regularization.jpg
• ‘혁펜하임 AI & 딥러닝 강의’ 선대 2-4강. 벡터의 norm 쉬운 설명
• ‘신박Ai’ [Deep Learning 101] L1, L2 Regularization