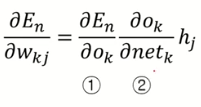*본 게시글은 유튜브 ‘김성범[ 교수 / 산업경영공학부 ]’ [ 핵심 머신러닝 ]뉴럴네트워크모델 2 (Backpropagation 알고리즘) 자료를 참고한 점임을 알립니다.
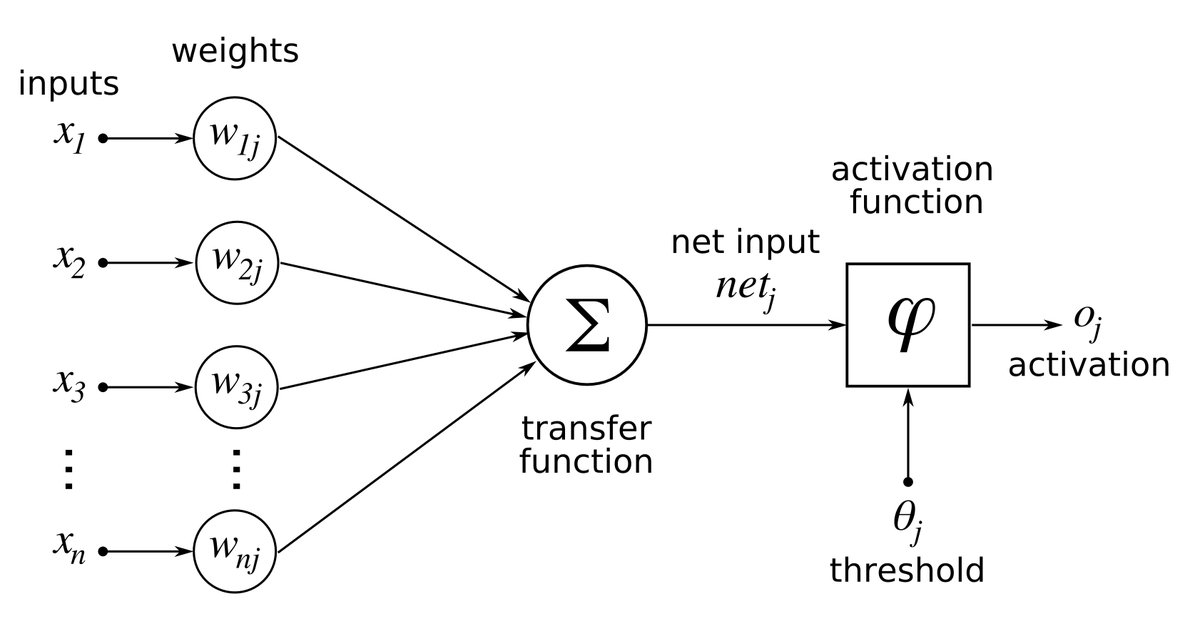
Neural Network
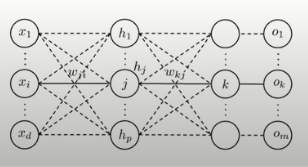
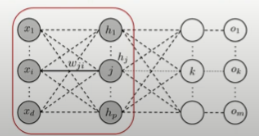
1. 전체 뉴럴 네트워크 정의
- 한번에 바로 미분하기에는 복잡
- 출력층과 은닉층, 은닉층과 입력층 단위로 구분
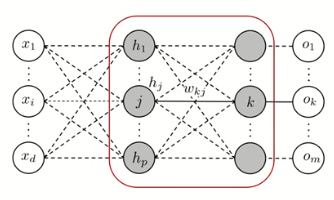
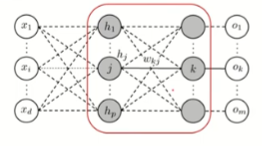
2. 출력층과 은닉층 사이
\[net_k = h_1 w_{k1} + h_2 w_{k2} + \cdots + h_j w_{kj} + \cdots + h_p w_{kp} + w_{k0}\] \[o_k = sigmoid(net_k) = \frac{1}{1 + \exp(-net_k)}\] \[E_n(w) = \frac{1}{2} \sum_{n=1}^{m} (t_k - o_k)^2\]
- Backpropagation를 통해 \(w_{kj}\)을 업데이트 하기 위해 \(\Delta w_{kj} = - \alpha \frac{\partial E_n}{\partial w_{kj}}\)를 계산
\[\frac{\partial E_n}{\partial w_{kj}} = \frac{\partial E_n}{\partial net_k} \frac{\partial net_k}{\partial w_{kj}} = \frac{\partial E_n}{\partial o_k} \frac{\partial o_k}{\partial net_k} \frac{\partial net_k}{\partial w_{kj}} = \frac{\partial E_n}{\partial o_k} \frac{\partial o_k}{\partial net_k} h_j\]
\[1.\frac{\partial E_n}{\partial o_k} = \frac{\partial}{\partial o_k} \frac{1}{2} \sum_{k=1}^m (t_k - o_k)^2 = \frac{\partial}{\partial o_k} \frac{1}{2} (t_k - o_k)^2 = -(t_k - o_k)\] \[2.\frac{\partial o_k}{\partial net_k} = \frac{\partial}{\partial net_k} \left( \frac{1}{1 + \exp(-net_k)} \right) = \frac{ -(-\exp(-net_k)) }{ (1 + \exp(-net_k))^2 } = \frac{ \exp(-net_k) }{ (1 + \exp(-net_k))^2 }\] \[\frac{\partial o_k}{\partial net_k} = o_k (1 - o_k)\] \[*(\,\sigma\,함수\,편미분의\,특징)\]
- 최종적으로 가중치를 업데이트할 때
\(\Delta w_{kj} = -\alpha \frac{\partial E_n}{\partial w_{kj}} = \alpha (t_k - o_k) o_k (1 - o_k) h_j\)
\[(\alpha:학습률,\,t_{k} : 실제값,\,o_{k}:예측값\,h_{j}:은닉층logit값)\]
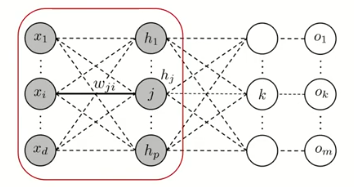
3. 은닉층과 입력층 사이
- Forward 진행 과정 \(net_j = x_1 w_{j1} + x_2 w_{j2} + \cdots + x_i w_{ji} + \cdots + x_d w_{jd} + w_{j0}\)
\[h_j = sigmoid(net_j) = \frac{1}{1 + \exp(-net_j)}\] \[net_k = h_1 w_{k1} + h_2 w_{k2} + \cdots + h_j w_{kj} + \cdots + h_p w_{kp} + w_{k0}\] \[o_k = sigmoid(net_k) = \frac{1}{1 + \exp(-net_k)}\] \[E_n(w) = \frac{1}{2} \sum_{n=1}^m (t_k - o_k)^2\]
- Backpropagation를 통해 \(w_{ji}\)을 업데이트 하기 위해 \(\Delta w_{ji} = - \alpha \frac{\partial E_n}{\partial w_{ji}}\)를 계산
\[\frac{\partial E_n}{\partial w_{ji}} = \frac{\partial E_n}{\partial net_j} \frac{\partial net_j}{\partial w_{ji}} = \frac{\partial E_n}{\partial net_j} x_i\]
\[\frac{\partial E_n}{\partial w_{ji}} = \frac{\partial E_n}{\partial net_j} x_i\] \[\frac{\partial E_n}{\partial net_j} = \frac{\partial}{\partial net_j} \left( \frac{1}{2} \sum_{k=1}^m (t_k - o_k)^2 \right) = \frac{1}{2} \sum_{k=1}^m \frac{\partial}{\partial net_j} (t_k - o_k)^2\] \[\frac{\partial E_n}{\partial net_j} = \frac{1}{2} \sum_{k=1}^m \frac{\partial (t_k - o_k)^2}{\partial net_j}\] \[= \frac{1}{2} \sum_{k=1}^m \frac{\partial (t_k - o_k)^2}{\partial o_k} \frac{\partial o_k}{\partial net_k} \frac{\partial net_k}{\partial h_j} \frac{\partial h_j}{\partial net_j}\] \[= \sum_{k=1}^m (t_k - o_k) \left( - \frac{\partial o_k}{\partial net_k} \frac{\partial net_k}{\partial h_j} \frac{\partial h_j}{\partial net_j} \right)\]
- 위 수식을 구체적으로 풀어쓰자면 \(1.\frac{\partial h_j}{\partial net_j} = h_j (1 - h_j)\)
\[*(\,\sigma\,함수\,편미분의\,특징)\] \[2.\frac{\partial net_k}{\partial h_j} = w_{kj}\] \[3.\frac{\partial o_k}{\partial net_k} = o_k (1 - o_k)\] \[*(\,\sigma\,함수\,편미분의\,특징)\]
\[\frac{\partial E_n}{\partial net_j} = -h_j (1 - h_j) \sum_{k=1}^m w_{kj} o_k (1 - o_k) (t_k - o_k)\]
\[\Delta w_{ji} = -\alpha \frac{\partial E_n}{\partial w_{ji}} = -\alpha \left( \frac{\partial E_n}{\partial net_j} x_i \right)\] \[\Delta w_{ji} = \alpha x_i h_j (1 - h_j) \sum_{k=1}^m w_{kj} o_k (1 - o_k) (t_k - o_k)\] \[(\alpha:학습률,\,x_{i}:입력값,\,h_{j}:은닉층\,logit값,w_{kj}:은닉층\, weight\,값,\,o_{k}:예측값,\,t_{k} : 실제값)\]
4. 출력층과 은닉층 / 은닉층과 입력층 \(\Delta w\) 정리
\[\Delta w_{kj} = -\alpha \frac{\partial E_n}{\partial w_{kj}}\] \[= \alpha (t_k - o_k) o_k (1 - o_k) h_j\]
\[\Delta w_{ji} = -\alpha \frac{\partial E_n}{\partial w_{ji}}\] \[= \alpha x_i h_j (1 - h_j) \sum_{k=1}^m w_{kj} o_k (1 - o_k) (t_k - o_k)\]
참고 자료